개발 공부 - [그래프 알고리즘] 순회 - 최소비용신장트리(minimum spanning tree) - 4

 prim의 알고리즘

임의의 노드를 출발노드로 선택

출발 노드를 포함하는 트리를 점점 키워 감

매 단계에서 이미 트리에 포함된 노드와 포함되지 않은 노드를 연결하는 에지들 중 가장 가중치가 작은 에지를 선택

Prim 알고리즘의 동작

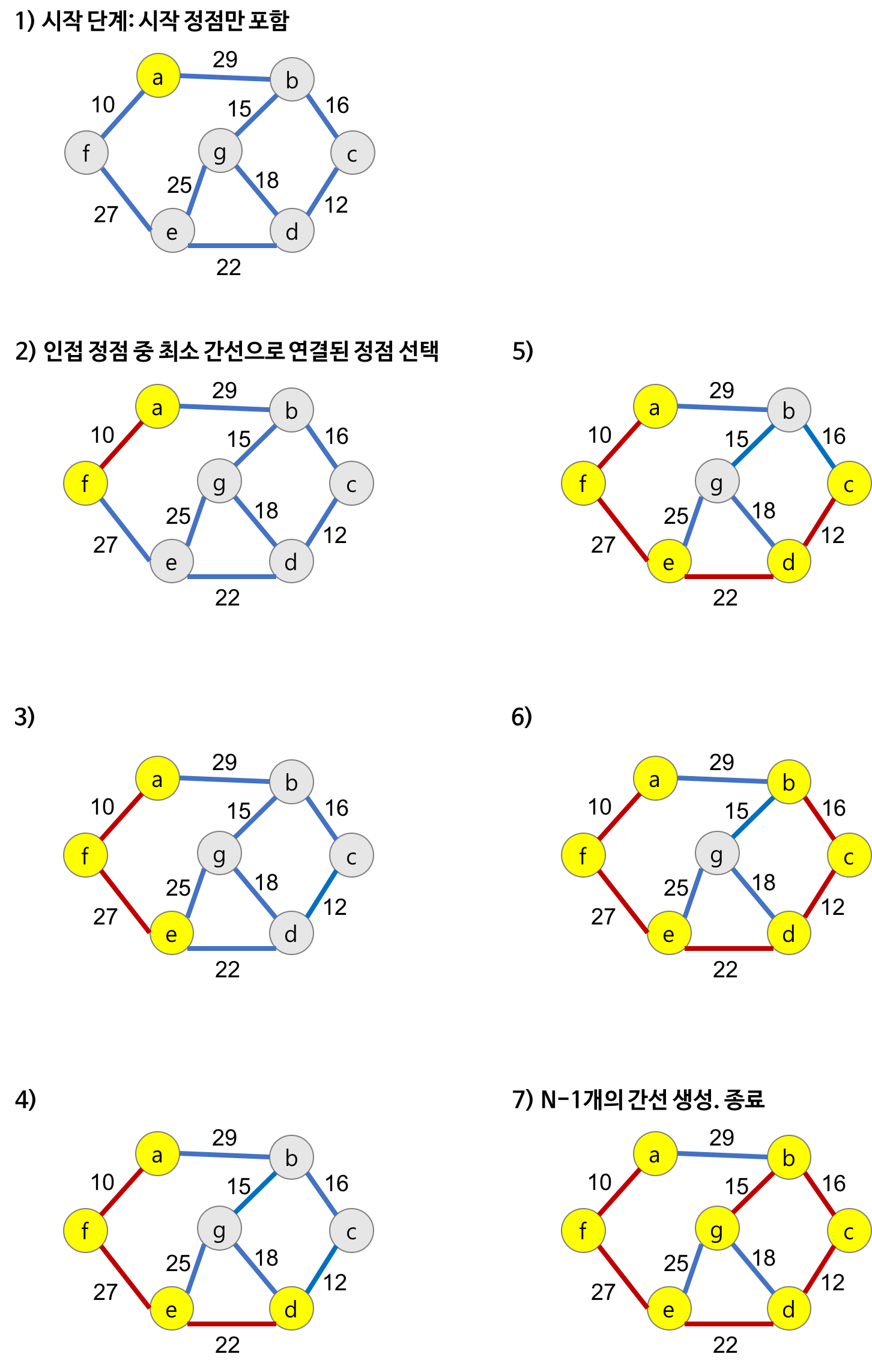
시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.

앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.

즉, 가장 낮은 가중치를 먼저 선택한다.

위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.

Prim 알고리즘의 구체적인 동작 과정

Prim 알고리즘을 이용하여 MST(최소 비용 신장 트리)를 만드는 과정

정점 선택을 기반 으로 하는 알고리즘

이전 단계에서 만들어진 신장 트리를 확장하는 방법

출처 : https://gmlwjd9405.github.io/2018/08/30/algorithm-prim-mst.html

왜 MST가 찾아지는가?

Prim의 알고리즘의 임의의 한 단계를 생각해 보면,

A를 현재까지 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정하자.

출발 노드에 이미 연결된 노드와 그렇지 않은 노드를 연결하는 에지들 중 lightest edge 를 찾을 수 있다.

가중치가 최소인 에지 찾기

V(A) : 이미 트리에 포함된 노드들

V(A) 에 아직 속하지 않은 각 노드 v에 대해서 다음과 같은 값을 유지

key(v) : 이미 V(A) 에 속한 노드와 자신을 연결하는 에지들 중 가중치가 최소인 에지 (u, v)의 가중치

ㅠ(v) : 그 에지 (u, v)의 끝점 u

가중치가 최소인 에지를 찾는 대신 key값이 최소인 노드를 찾는다.

* ㅠ[f]는 파이오브 에프 라고 읽는 것이군...

key 값이 최소인 노드 f를 찾고, 에지 (f, ㅠ(f))를 선택한다.

노드 d, g, e의 key 값과 ㅠ값을 갱신한다.

MST-PRIM(G, w, r)
    for each u <= V do
        key[u] <- zero
        ㅠ[u] <- NIL
    end.
    V(A) <- {r}
    key[r] <- 0
    while |V(A)| < n do // while문은 n-1번 반복
        find u <=/ V(A) with the minimum key value; // 최소값 찾기 O(n)
        V(A) <- V(A) U {u}
        for each V <=/ V(A) adjacent to u do
            if key[v] > w(u, v) then
                key[v] <- w(u, v)
                ㅠ[v] <- u
            end.
        end.
    end.

• 시간복잡도 O(n^2)

참조: https://mj-seok.com/algorithm/algo-prim/

key 값이 최소인 원소를 찾기

• 최소 우선순위 큐를 사용
  • V - V(A)에 속한 노드들을 저장
  • Extract-Min : key값이 최소인

MST-PRIM(G, w, r)
    for each u <= V[G]
        do key[u] <- Infinity
            ㅠ[u] <- NIL
    key[r] <- 0
    Q <- V[G]
    while Q =/ zero
        do u <- EXTRACT-MIN(Q)
            for each v <= Adj[u]
                do if v <= Q and w(u, v) < key[v]
                    then ㅠ[v] <- u
                        key[v] <- w(u, v)
                        // 우선순위큐에서 key값 decrease: O(logn)

Prim의 알고리즘 : 시간복잡도

• 이진 힙(binary heap)을 사용하여 우선순위 큐를 구현한 경우
• while loop:
  • n번의 Extract-Min 연산 : O(nlogn)
  • m번의 Decrease-Key 연산 : O(mlogn)
• 따라서 시간복잡도 : O(nlogn + mlogn) = O(mlogn)
• 우선순위 큐를 사용하지 않고 단순하게 구현할 경우 : O(n^2)
• Fibonacci 힙을 사용하여 O(m + nlogn)에 구현가능[Fredman-Tarjan 1984]

참조: https://mj-seok.com/algorithm/algo-prim/

어떤게 좋다고 말할수는 없는데 최악/최선의 경우를 설명해 주시는 것

-.-)... 허...허프만 부터는 제정신을 잡고 열심히 하겄읍니다...

O(n^2) 보다 저 피보나치 힙 사용해서 구현하는 편이 낫다고 하심...